Tutorial#
Note
An interactive version of the tutorial is available via Google Colab.
Colour spreads over various domains of Colour Science, from colour models to optical phenomena, this tutorial does not give a complete overview of the API but is a good introduction to the main concepts.
Note
A directory with examples is available at this path in Colour installation: colour/examples. It can also be explored directly on Github.
from colour.plotting import *
colour_style()
plot_visible_spectrum()

Overview#
Colour is organised around various sub-packages:
adaptation: Chromatic adaptation models and transformations.
algebra: Algebra utilities.
appearance: Colour appearance models.
biochemistry: Biochemistry computations.
blindness: Colour vision deficiency models.
characterisation: Colour correction, camera and display characterisation.
colorimetry: Core objects for colour computations.
constants: CIE and CODATA constants.
continuous: Base objects for continuous data representation.
contrast: Objects for contrast sensitivity computation.
corresponding: Corresponding colour chromaticities computations.
difference: Colour difference computations.
geometry: Geometry primitives generation.
graph: Graph for automatic colour conversions.
hints: Type hints for annotations.
io: Input / output objects for reading and writing data.
models: Colour models.
notation: Colour notation systems.
phenomena: Computation of various optical phenomena.
plotting: Diagrams, figures, etc…
quality: Colour quality computation.
recovery: Reflectance recovery.
temperature: Colour temperature and correlated colour temperature computation.
utilities: Various utilities and data structures.
volume: Colourspace volumes computation and optimal colour stimuli.
Most of the public API is available from the root colour namespace:
import colour
print(colour.__all__[:5] + ["..."])
['domain_range_scale', 'get_domain_range_scale', 'set_domain_range_scale', 'CHROMATIC_ADAPTATION_METHODS', 'CHROMATIC_ADAPTATION_TRANSFORMS', '...']
The various sub-packages also expose their public API:
from pprint import pprint
for sub_package in (
"adaptation",
"algebra",
"appearance",
"biochemistry",
"blindness",
"characterisation",
"colorimetry",
"constants",
"continuous",
"contrast",
"corresponding",
"difference",
"geometry",
"graph",
"hints",
"io",
"models",
"notation",
"phenomena",
"plotting",
"quality",
"recovery",
"temperature",
"utilities",
"volume",
):
print(sub_package.title())
pprint(getattr(colour, sub_package).__all__[:5] + ["..."])
print("\n")
Adaptation
['CHROMATIC_ADAPTATION_TRANSFORMS',
'CAT_BIANCO2010',
'CAT_BRADFORD',
'CAT_CAT02',
'CAT_CAT02_BRILL2008',
'...']
Algebra
['get_sdiv_mode',
'set_sdiv_mode',
'sdiv_mode',
'sdiv',
'is_spow_enabled',
'...']
Appearance
['InductionFactors_Hunt',
'VIEWING_CONDITIONS_HUNT',
'CAM_Specification_Hunt',
'XYZ_to_Hunt',
'CAM_Specification_ATD95',
'...']
Biochemistry
['REACTION_RATE_MICHAELISMENTEN_METHODS',
'reaction_rate_MichaelisMenten',
'SUBSTRATE_CONCENTRATION_MICHAELISMENTEN_METHODS',
'substrate_concentration_MichaelisMenten',
'reaction_rate_MichaelisMenten_Michaelis1913',
'...']
Blindness
['CVD_MATRICES_MACHADO2010',
'msds_cmfs_anomalous_trichromacy_Machado2009',
'matrix_anomalous_trichromacy_Machado2009',
'matrix_cvd_Machado2009',
'...']
Characterisation
['RGB_CameraSensitivities',
'RGB_DisplayPrimaries',
'MSDS_ACES_RICD',
'MSDS_CAMERA_SENSITIVITIES',
'CCS_COLOURCHECKERS',
'...']
Colorimetry
['SpectralShape',
'SPECTRAL_SHAPE_DEFAULT',
'SpectralDistribution',
'MultiSpectralDistributions',
'reshape_sd',
'...']
Constants
['CONSTANT_K_M',
'CONSTANT_KP_M',
'CONSTANT_AVOGADRO',
'CONSTANT_BOLTZMANN',
'CONSTANT_LIGHT_SPEED',
'...']
Continuous
['AbstractContinuousFunction', 'Signal', 'MultiSignals', '...']
Contrast
['optical_MTF_Barten1999',
'pupil_diameter_Barten1999',
'sigma_Barten1999',
'retinal_illuminance_Barten1999',
'maximum_angular_size_Barten1999',
'...']
Corresponding
['BRENEMAN_EXPERIMENTS',
'BRENEMAN_EXPERIMENT_PRIMARIES_CHROMATICITIES',
'CorrespondingColourDataset',
'CorrespondingChromaticitiesPrediction',
'corresponding_chromaticities_prediction_CIE1994',
'...']
Difference
['delta_E_CAM02LCD',
'delta_E_CAM02SCD',
'delta_E_CAM02UCS',
'delta_E_CAM16LCD',
'delta_E_CAM16SCD',
'...']
Geometry
['ellipse_coefficients_general_form',
'ellipse_coefficients_canonical_form',
'point_at_angle_on_ellipse',
'ellipse_fitting_Halir1998',
'ELLIPSE_FITTING_METHODS',
'...']
Graph
['CONVERSION_GRAPH',
'CONVERSION_GRAPH_NODE_LABELS',
'describe_conversion_path',
'convert',
'...']
Hints
['ArrayLike', 'NDArray', 'ModuleType', 'Any', 'Callable', '...']
Io
['LUT1D',
'LUT3x1D',
'LUT3D',
'LUT_to_LUT',
'AbstractLUTSequenceOperator',
'...']
Models
['COLOURSPACE_MODELS',
'COLOURSPACE_MODELS_AXIS_LABELS',
'COLOURSPACE_MODELS_DOMAIN_RANGE_SCALE_1_TO_REFERENCE',
'Jab_to_JCh',
'JCh_to_Jab',
'...']
Notation
['CSS_COLOR_3_BASIC',
'CSS_COLOR_3_EXTENDED',
'CSS_COLOR_3',
'MUNSELL_COLOURS_ALL',
'MUNSELL_COLOURS_1929',
'...']
Phenomena
['scattering_cross_section',
'rayleigh_optical_depth',
'rayleigh_scattering',
'sd_rayleigh_scattering',
'...']
Plotting
['SD_ASTMG173_ETR',
'SD_ASTMG173_GLOBAL_TILT',
'SD_ASTMG173_DIRECT_CIRCUMSOLAR',
'CONSTANTS_COLOUR_STYLE',
'CONSTANTS_ARROW_STYLE',
'...']
Quality
['SDS_TCS',
'SDS_VS',
'ColourRendering_Specification_CIE2017',
'colour_fidelity_index_CIE2017',
'ColourQuality_Specification_ANSIIESTM3018',
'...']
Recovery
['SPECTRAL_SHAPE_BASIS_FUNCTIONS_DYER2017',
'BASIS_FUNCTIONS_DYER2017',
'SPECTRAL_SHAPE_sRGB_MALLETT2019',
'MSDS_BASIS_FUNCTIONS_sRGB_MALLETT2019',
'SPECTRAL_SHAPE_OTSU2018',
'...']
Temperature
['xy_to_CCT_CIE_D',
'CCT_to_xy_CIE_D',
'xy_to_CCT_Hernandez1999',
'CCT_to_xy_Hernandez1999',
'xy_to_CCT_Kang2002',
'...']
Utilities
['Lookup',
'Structure',
'CanonicalMapping',
'LazyCanonicalMapping',
'Node',
'...']
Volume
['OPTIMAL_COLOUR_STIMULI_ILLUMINANTS',
'is_within_macadam_limits',
'is_within_mesh_volume',
'is_within_pointer_gamut',
'generate_pulse_waves',
'...']
The codebase is documented and most docstrings have usage examples:
print(colour.temperature.CCT_to_uv_Ohno2013.__doc__)
Return the *CIE UCS* colourspace *uv* chromaticity coordinates from given
correlated colour temperature :math:`T_{cp}`, :math:`\Delta_{uv}` and
colour matching functions using *Ohno (2013)* method.
Parameters
----------
CCT_D_uv
Correlated colour temperature :math:`T_{cp}`, :math:`\Delta_{uv}`.
cmfs
Standard observer colour matching functions, default to the
*CIE 1931 2 Degree Standard Observer*.
Returns
-------
:class:`numpy.ndarray`
*CIE UCS* colourspace *uv* chromaticity coordinates.
References
----------
:cite:`Ohno2014a`
Examples
--------
from colour import MSDS_CMFS, SPECTRAL_SHAPE_DEFAULT
cmfs = (
MSDS_CMFS["CIE 1931 2 Degree Standard Observer"]
.copy()
.align(SPECTRAL_SHAPE_DEFAULT)
)
CCT_D_uv = np.array([6507.4342201047066, 0.003223690901513])
CCT_to_uv_Ohno2013(CCT_D_uv, cmfs) # doctest: +ELLIPSIS
array([ 0.1977999..., 0.3122004...])
At the core of Colour is the colour.colorimetry sub-package, it defines
the objects needed for spectral computations and many others:
pprint(colour.colorimetry.__all__)
['SpectralShape',
'SPECTRAL_SHAPE_DEFAULT',
'SpectralDistribution',
'MultiSpectralDistributions',
'reshape_sd',
'reshape_msds',
'sds_and_msds_to_sds',
'sds_and_msds_to_msds',
'planck_law',
'blackbody_spectral_radiance',
'sd_blackbody',
'rayleigh_jeans_law',
'sd_rayleigh_jeans',
'LMS_ConeFundamentals',
'RGB_ColourMatchingFunctions',
'XYZ_ColourMatchingFunctions',
'CCS_ILLUMINANTS',
'MSDS_CMFS',
'MSDS_CMFS_LMS',
'MSDS_CMFS_RGB',
'MSDS_CMFS_STANDARD_OBSERVER',
'SDS_BASIS_FUNCTIONS_CIE_ILLUMINANT_D_SERIES',
'SDS_ILLUMINANTS',
'SDS_LEFS',
'SDS_LEFS_PHOTOPIC',
'SDS_LEFS_SCOTOPIC',
'TVS_ILLUMINANTS',
'TVS_ILLUMINANTS_HUNTERLAB',
'CCS_LIGHT_SOURCES',
'SDS_LIGHT_SOURCES',
'sd_constant',
'sd_zeros',
'sd_ones',
'msds_constant',
'msds_zeros',
'msds_ones',
'SD_GAUSSIAN_METHODS',
'sd_gaussian',
'sd_gaussian_normal',
'sd_gaussian_fwhm',
'SD_SINGLE_LED_METHODS',
'sd_single_led',
'sd_single_led_Ohno2005',
'SD_MULTI_LEDS_METHODS',
'sd_multi_leds',
'sd_multi_leds_Ohno2005',
'SD_TO_XYZ_METHODS',
'MSDS_TO_XYZ_METHODS',
'sd_to_XYZ',
'msds_to_XYZ',
'SPECTRAL_SHAPE_ASTME308',
'handle_spectral_arguments',
'lagrange_coefficients_ASTME2022',
'tristimulus_weighting_factors_ASTME2022',
'adjust_tristimulus_weighting_factors_ASTME308',
'sd_to_XYZ_integration',
'sd_to_XYZ_tristimulus_weighting_factors_ASTME308',
'sd_to_XYZ_ASTME308',
'msds_to_XYZ_integration',
'msds_to_XYZ_ASTME308',
'wavelength_to_XYZ',
'spectral_uniformity',
'BANDPASS_CORRECTION_METHODS',
'bandpass_correction',
'bandpass_correction_Stearns1988',
'sd_CIE_standard_illuminant_A',
'sd_CIE_illuminant_D_series',
'daylight_locus_function',
'sd_mesopic_luminous_efficiency_function',
'mesopic_weighting_function',
'LIGHTNESS_METHODS',
'lightness',
'lightness_Glasser1958',
'lightness_Wyszecki1963',
'lightness_CIE1976',
'lightness_Fairchild2010',
'lightness_Fairchild2011',
'lightness_Abebe2017',
'intermediate_lightness_function_CIE1976',
'LUMINANCE_METHODS',
'luminance',
'luminance_Newhall1943',
'luminance_ASTMD1535',
'luminance_CIE1976',
'luminance_Fairchild2010',
'luminance_Fairchild2011',
'luminance_Abebe2017',
'intermediate_luminance_function_CIE1976',
'dominant_wavelength',
'complementary_wavelength',
'excitation_purity',
'colorimetric_purity',
'luminous_flux',
'luminous_efficiency',
'luminous_efficacy',
'RGB_10_degree_cmfs_to_LMS_10_degree_cmfs',
'RGB_2_degree_cmfs_to_XYZ_2_degree_cmfs',
'RGB_10_degree_cmfs_to_XYZ_10_degree_cmfs',
'LMS_2_degree_cmfs_to_XYZ_2_degree_cmfs',
'LMS_10_degree_cmfs_to_XYZ_10_degree_cmfs',
'WHITENESS_METHODS',
'whiteness',
'whiteness_Berger1959',
'whiteness_Taube1960',
'whiteness_Stensby1968',
'whiteness_ASTME313',
'whiteness_Ganz1979',
'whiteness_CIE2004',
'YELLOWNESS_METHODS',
'yellowness',
'yellowness_ASTMD1925',
'yellowness_ASTME313_alternative',
'YELLOWNESS_COEFFICIENTS_ASTME313',
'yellowness_ASTME313']
Colour computations leverage a comprehensive quantity of datasets available
in most sub-packages, for example the colour.colorimetry.datasets defines
the following components:
pprint(colour.colorimetry.datasets.__all__)
['MSDS_CMFS',
'MSDS_CMFS_LMS',
'MSDS_CMFS_RGB',
'MSDS_CMFS_STANDARD_OBSERVER',
'CCS_ILLUMINANTS',
'SDS_BASIS_FUNCTIONS_CIE_ILLUMINANT_D_SERIES',
'TVS_ILLUMINANTS_HUNTERLAB',
'SDS_ILLUMINANTS',
'TVS_ILLUMINANTS',
'CCS_LIGHT_SOURCES',
'SDS_LIGHT_SOURCES',
'SDS_LEFS',
'SDS_LEFS_PHOTOPIC',
'SDS_LEFS_SCOTOPIC']
From Spectral Distribution#
Whether it be a sample spectral distribution, colour matching functions or
illuminants, spectral data is manipulated using an object built with the
colour.SpectralDistribution class or based on it:
# Defining a sample spectral distribution data.
data_sample = {
380: 0.048,
385: 0.051,
390: 0.055,
395: 0.060,
400: 0.065,
405: 0.068,
410: 0.068,
415: 0.067,
420: 0.064,
425: 0.062,
430: 0.059,
435: 0.057,
440: 0.055,
445: 0.054,
450: 0.053,
455: 0.053,
460: 0.052,
465: 0.052,
470: 0.052,
475: 0.053,
480: 0.054,
485: 0.055,
490: 0.057,
495: 0.059,
500: 0.061,
505: 0.062,
510: 0.065,
515: 0.067,
520: 0.070,
525: 0.072,
530: 0.074,
535: 0.075,
540: 0.076,
545: 0.078,
550: 0.079,
555: 0.082,
560: 0.087,
565: 0.092,
570: 0.100,
575: 0.107,
580: 0.115,
585: 0.122,
590: 0.129,
595: 0.134,
600: 0.138,
605: 0.142,
610: 0.146,
615: 0.150,
620: 0.154,
625: 0.158,
630: 0.163,
635: 0.167,
640: 0.173,
645: 0.180,
650: 0.188,
655: 0.196,
660: 0.204,
665: 0.213,
670: 0.222,
675: 0.231,
680: 0.242,
685: 0.251,
690: 0.261,
695: 0.271,
700: 0.282,
705: 0.294,
710: 0.305,
715: 0.318,
720: 0.334,
725: 0.354,
730: 0.372,
735: 0.392,
740: 0.409,
745: 0.420,
750: 0.436,
755: 0.450,
760: 0.462,
765: 0.465,
770: 0.448,
775: 0.432,
780: 0.421,
}
sd = colour.SpectralDistribution(data_sample, name="Sample")
print(repr(sd))
SpectralDistribution([[ 3.80000000e+02, 4.80000000e-02],
[ 3.85000000e+02, 5.10000000e-02],
[ 3.90000000e+02, 5.50000000e-02],
[ 3.95000000e+02, 6.00000000e-02],
[ 4.00000000e+02, 6.50000000e-02],
[ 4.05000000e+02, 6.80000000e-02],
[ 4.10000000e+02, 6.80000000e-02],
[ 4.15000000e+02, 6.70000000e-02],
[ 4.20000000e+02, 6.40000000e-02],
[ 4.25000000e+02, 6.20000000e-02],
[ 4.30000000e+02, 5.90000000e-02],
[ 4.35000000e+02, 5.70000000e-02],
[ 4.40000000e+02, 5.50000000e-02],
[ 4.45000000e+02, 5.40000000e-02],
[ 4.50000000e+02, 5.30000000e-02],
[ 4.55000000e+02, 5.30000000e-02],
[ 4.60000000e+02, 5.20000000e-02],
[ 4.65000000e+02, 5.20000000e-02],
[ 4.70000000e+02, 5.20000000e-02],
[ 4.75000000e+02, 5.30000000e-02],
[ 4.80000000e+02, 5.40000000e-02],
[ 4.85000000e+02, 5.50000000e-02],
[ 4.90000000e+02, 5.70000000e-02],
[ 4.95000000e+02, 5.90000000e-02],
[ 5.00000000e+02, 6.10000000e-02],
[ 5.05000000e+02, 6.20000000e-02],
[ 5.10000000e+02, 6.50000000e-02],
[ 5.15000000e+02, 6.70000000e-02],
[ 5.20000000e+02, 7.00000000e-02],
[ 5.25000000e+02, 7.20000000e-02],
[ 5.30000000e+02, 7.40000000e-02],
[ 5.35000000e+02, 7.50000000e-02],
[ 5.40000000e+02, 7.60000000e-02],
[ 5.45000000e+02, 7.80000000e-02],
[ 5.50000000e+02, 7.90000000e-02],
[ 5.55000000e+02, 8.20000000e-02],
[ 5.60000000e+02, 8.70000000e-02],
[ 5.65000000e+02, 9.20000000e-02],
[ 5.70000000e+02, 1.00000000e-01],
[ 5.75000000e+02, 1.07000000e-01],
[ 5.80000000e+02, 1.15000000e-01],
[ 5.85000000e+02, 1.22000000e-01],
[ 5.90000000e+02, 1.29000000e-01],
[ 5.95000000e+02, 1.34000000e-01],
[ 6.00000000e+02, 1.38000000e-01],
[ 6.05000000e+02, 1.42000000e-01],
[ 6.10000000e+02, 1.46000000e-01],
[ 6.15000000e+02, 1.50000000e-01],
[ 6.20000000e+02, 1.54000000e-01],
[ 6.25000000e+02, 1.58000000e-01],
[ 6.30000000e+02, 1.63000000e-01],
[ 6.35000000e+02, 1.67000000e-01],
[ 6.40000000e+02, 1.73000000e-01],
[ 6.45000000e+02, 1.80000000e-01],
[ 6.50000000e+02, 1.88000000e-01],
[ 6.55000000e+02, 1.96000000e-01],
[ 6.60000000e+02, 2.04000000e-01],
[ 6.65000000e+02, 2.13000000e-01],
[ 6.70000000e+02, 2.22000000e-01],
[ 6.75000000e+02, 2.31000000e-01],
[ 6.80000000e+02, 2.42000000e-01],
[ 6.85000000e+02, 2.51000000e-01],
[ 6.90000000e+02, 2.61000000e-01],
[ 6.95000000e+02, 2.71000000e-01],
[ 7.00000000e+02, 2.82000000e-01],
[ 7.05000000e+02, 2.94000000e-01],
[ 7.10000000e+02, 3.05000000e-01],
[ 7.15000000e+02, 3.18000000e-01],
[ 7.20000000e+02, 3.34000000e-01],
[ 7.25000000e+02, 3.54000000e-01],
[ 7.30000000e+02, 3.72000000e-01],
[ 7.35000000e+02, 3.92000000e-01],
[ 7.40000000e+02, 4.09000000e-01],
[ 7.45000000e+02, 4.20000000e-01],
[ 7.50000000e+02, 4.36000000e-01],
[ 7.55000000e+02, 4.50000000e-01],
[ 7.60000000e+02, 4.62000000e-01],
[ 7.65000000e+02, 4.65000000e-01],
[ 7.70000000e+02, 4.48000000e-01],
[ 7.75000000e+02, 4.32000000e-01],
[ 7.80000000e+02, 4.21000000e-01]],
interpolator=SpragueInterpolator,
interpolator_args={},
extrapolator=Extrapolator,
extrapolator_args={u'right': None, u'method': u'Constant', u'left': None})
The sample spectral distribution can be easily plotted against the visible spectrum:
# Plotting the sample spectral distribution.
plot_single_sd(sd)
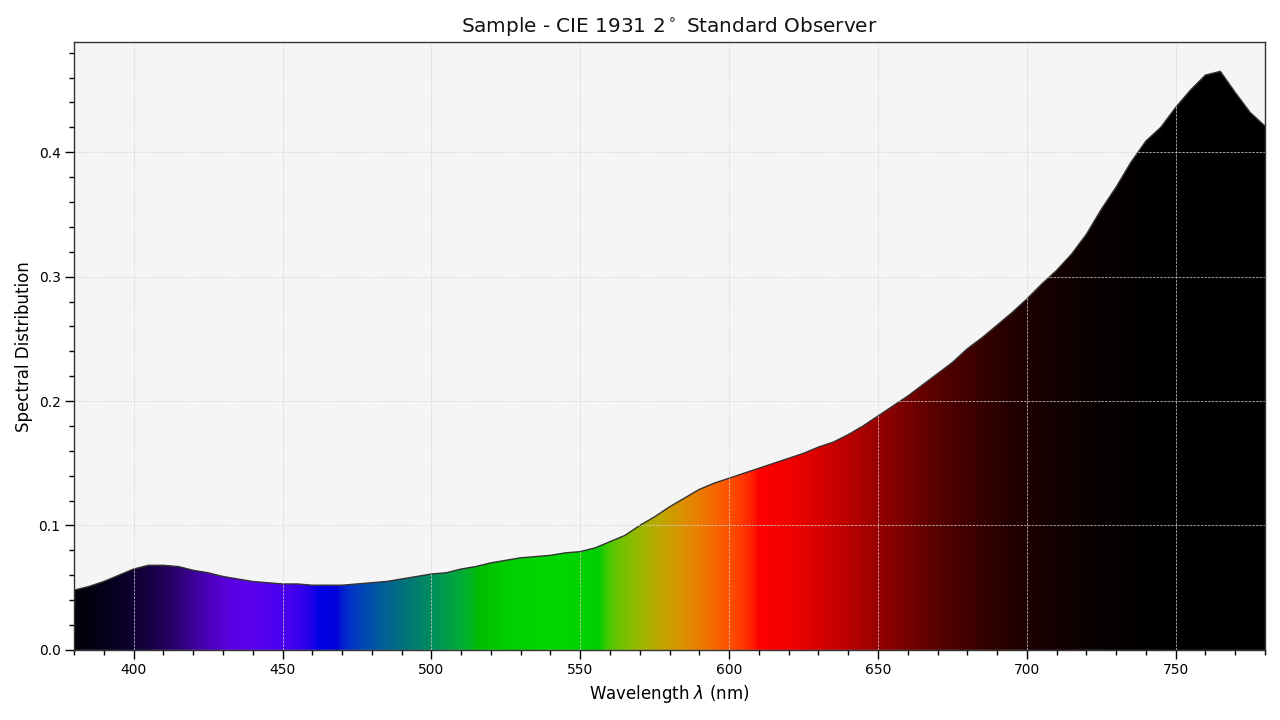
With the sample spectral distribution defined, its shape is retrieved as follows:
# Displaying the sample spectral distribution shape.
print(sd.shape)
(380.0, 780.0, 5.0)
The returned shape is an instance of the colour.SpectralShape class:
repr(sd.shape)
'SpectralShape(380.0, 780.0, 5.0)'
The colour.SpectralShape class is used throughout Colour to define
spectral dimensions and is instantiated as follows:
# Using *colour.SpectralShape* with iteration.
shape = colour.SpectralShape(start=0, end=10, interval=1)
for wavelength in shape:
print(wavelength)
# *colour.SpectralShape.wavelengths* property is providing the complete
# range of wavelengths.
shape = colour.SpectralShape(0, 10, 0.5)
shape.wavelengths
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
10.0
array([ 0. , 0.5, 1. , 1.5, 2. , 2.5, 3. , 3.5, 4. ,
4.5, 5. , 5.5, 6. , 6.5, 7. , 7.5, 8. , 8.5,
9. , 9.5, 10. ])
Colour defines three convenient objects to create constant spectral distributions:
colour.sd_constantcolour.sd_zeroscolour.sd_ones
# Defining a constant spectral distribution.
sd_constant = colour.sd_constant(100)
print('"Constant Spectral Distribution"')
print(sd_constant.shape)
print(sd_constant[400])
# Defining a zeros filled spectral distribution.
print('\n"Zeros Filled Spectral Distribution"')
sd_zeros = colour.sd_zeros()
print(sd_zeros.shape)
print(sd_zeros[400])
# Defining a ones filled spectral distribution.
print('\n"Ones Filled Spectral Distribution"')
sd_ones = colour.sd_ones()
print(sd_ones.shape)
print(sd_ones[400])
"Constant Spectral Distribution"
(360.0, 780.0, 1.0)
100.0
"Zeros Filled Spectral Distribution"
(360.0, 780.0, 1.0)
0.0
"Ones Filled Spectral Distribution"
(360.0, 780.0, 1.0)
1.0
By default the shape used by colour.sd_constant,
colour.sd_zeros and colour.sd_ones is the one defined by the
colour.SPECTRAL_SHAPE_DEFAULT attribute and based on ASTM E308-15
practise shape.
print(repr(colour.SPECTRAL_SHAPE_DEFAULT))
SpectralShape(360, 780, 1)
A custom shape can be passed to construct a constant spectral distribution with user defined dimensions:
colour.sd_ones(colour.SpectralShape(400, 700, 5))[450]
1.0
The colour.SpectralDistribution class supports the following
arithmetical operations:
addition
subtraction
multiplication
division
exponentiation
sd1 = colour.sd_ones()
print('"Ones Filled Spectral Distribution"')
print(sd1[400])
print('\n"x2 Constant Multiplied"')
print((sd1 * 2)[400])
print('\n"+ Spectral Distribution"')
print((sd1 + colour.sd_ones())[400])
"Ones Filled Spectral Distribution"
1.0
"x2 Constant Multiplied"
2.0
"+ Spectral Distribution"
2.0
Often interpolation of the spectral distribution is required, this is achieved
with the colour.SpectralDistribution.interpolate method. Depending on the
wavelengths uniformity, the default interpolation method will differ.
Following CIE 167:2005 recommendation: The method developed by
Sprague (1880) should be used for interpolating functions having a uniformly
spaced independent variable and a Cubic Spline method for non-uniformly spaced
independent variable [CIET13805a].
The uniformity of the sample spectral distribution is assessed as follows:
# Checking the sample spectral distribution uniformity.
print(sd.is_uniform())
True
In this case, since the sample spectral distribution is uniform the
interpolation defaults to the colour.SpragueInterpolator interpolator.
Note
Interpolation happens in place and may alter the original data, use the
colour.SpectralDistribution.copy method to generate a copy of the
spectral distribution before interpolation.
# Copying the sample spectral distribution.
sd_copy = sd.copy()
# Interpolating the copied sample spectral distribution.
sd_copy.interpolate(colour.SpectralShape(400, 770, 1))
sd_copy[401]
0.065809599999999996
# Comparing the interpolated spectral distribution with the original one.
plot_multi_sds([sd, sd_copy], bounding_box=[730, 780, 0.25, 0.5])
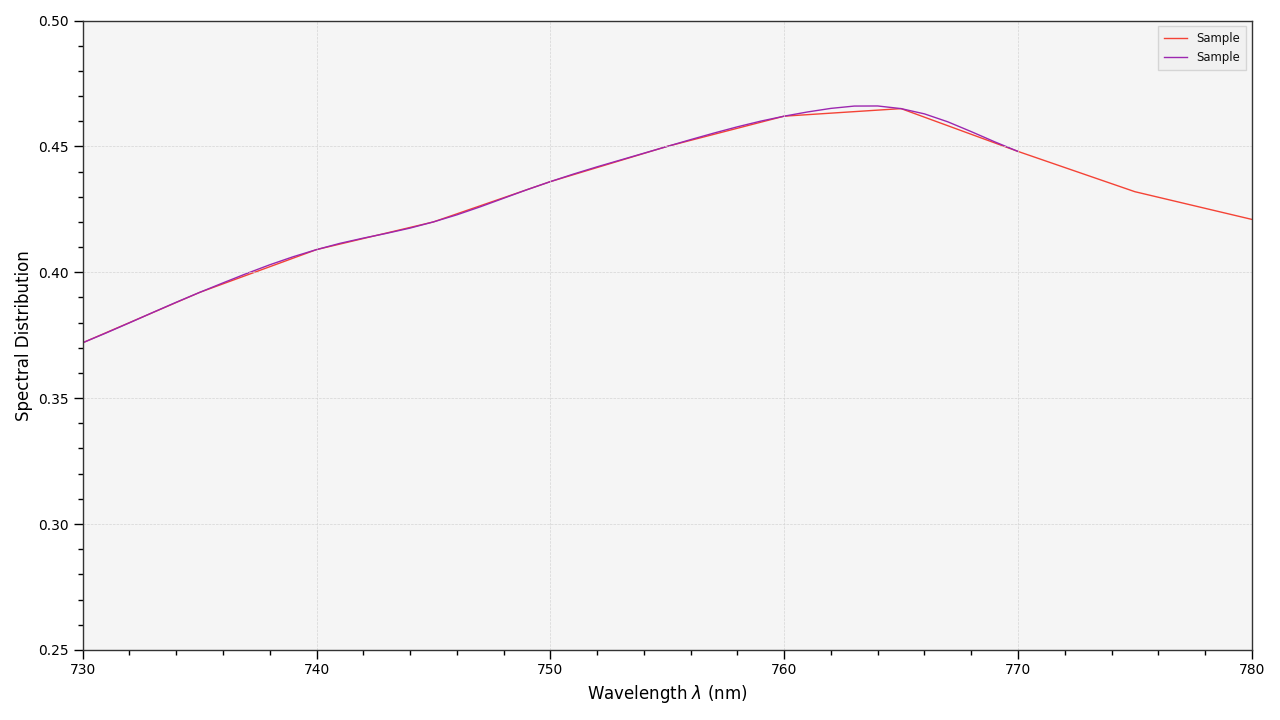
Extrapolation although dangerous can be used to help aligning two spectral distributions together. CIE publication CIE 15:2004 “Colorimetry” recommends that unmeasured values may be set equal to the nearest measured value of the appropriate quantity in truncation [CIET14804f]:
# Extrapolating the copied sample spectral distribution.
sd_copy.extrapolate(colour.SpectralShape(340, 830, 1))
sd_copy[340], sd_copy[830]
(0.065000000000000002, 0.44800000000000018)
The underlying interpolator can be swapped for any of the Colour interpolators:
pprint(
[
export
for export in colour.algebra.interpolation.__all__
if "Interpolator" in export
]
)
[u'KernelInterpolator',
u'LinearInterpolator',
u'SpragueInterpolator',
u'CubicSplineInterpolator',
u'PchipInterpolator',
u'NullInterpolator']
# Changing interpolator while trimming the copied spectral distribution.
sd_copy.interpolate(
colour.SpectralShape(400, 700, 10),
interpolator=colour.LinearInterpolator,
)
SpectralDistribution([[ 4.00000000e+02, 6.50000000e-02],
[ 4.10000000e+02, 6.80000000e-02],
[ 4.20000000e+02, 6.40000000e-02],
[ 4.30000000e+02, 5.90000000e-02],
[ 4.40000000e+02, 5.50000000e-02],
[ 4.50000000e+02, 5.30000000e-02],
[ 4.60000000e+02, 5.20000000e-02],
[ 4.70000000e+02, 5.20000000e-02],
[ 4.80000000e+02, 5.40000000e-02],
[ 4.90000000e+02, 5.70000000e-02],
[ 5.00000000e+02, 6.10000000e-02],
[ 5.10000000e+02, 6.50000000e-02],
[ 5.20000000e+02, 7.00000000e-02],
[ 5.30000000e+02, 7.40000000e-02],
[ 5.40000000e+02, 7.60000000e-02],
[ 5.50000000e+02, 7.90000000e-02],
[ 5.60000000e+02, 8.70000000e-02],
[ 5.70000000e+02, 1.00000000e-01],
[ 5.80000000e+02, 1.15000000e-01],
[ 5.90000000e+02, 1.29000000e-01],
[ 6.00000000e+02, 1.38000000e-01],
[ 6.10000000e+02, 1.46000000e-01],
[ 6.20000000e+02, 1.54000000e-01],
[ 6.30000000e+02, 1.63000000e-01],
[ 6.40000000e+02, 1.73000000e-01],
[ 6.50000000e+02, 1.88000000e-01],
[ 6.60000000e+02, 2.04000000e-01],
[ 6.70000000e+02, 2.22000000e-01],
[ 6.80000000e+02, 2.42000000e-01],
[ 6.90000000e+02, 2.61000000e-01],
[ 7.00000000e+02, 2.82000000e-01]],
interpolator=SpragueInterpolator,
interpolator_args={},
extrapolator=Extrapolator,
extrapolator_args={u'right': None, u'method': u'Constant', u'left': None})
The extrapolation behaviour can be changed for Linear method instead
of the Constant default method or even use arbitrary constant left
and right values:
# Extrapolating the copied sample spectral distribution with *Linear* method.
sd_copy.extrapolate(
colour.SpectralShape(340, 830, 1),
extrapolator_kwargs={"method": "Linear", "right": 0},
)
sd_copy[340], sd_copy[830]
(0.046999999999999348, 0.0)
Aligning a spectral distribution is a convenient way to first interpolates the current data within its original bounds, then, if required, extrapolate any missing values to match the requested shape:
# Aligning the cloned sample spectral distribution.
# The spectral distribution is first trimmed as above.
sd_copy.interpolate(colour.SpectralShape(400, 700, 1))
sd_copy.align(colour.SpectralShape(340, 830, 5))
sd_copy[340], sd_copy[830]
(0.065000000000000002, 0.28199999999999975)
The colour.SpectralDistribution class also supports various arithmetic
operations like addition, subtraction, multiplication, division or
exponentiation with numeric and array_like variables or other
colour.SpectralDistribution class instances:
sd = colour.SpectralDistribution(
{
410: 0.25,
420: 0.50,
430: 0.75,
440: 1.0,
450: 0.75,
460: 0.50,
480: 0.25,
}
)
print((sd.copy() + 1).values)
print((sd.copy() * 2).values)
print((sd * [0.35, 1.55, 0.75, 2.55, 0.95, 0.65, 0.15]).values)
print((sd * colour.sd_constant(2, sd.shape) * colour.sd_constant(3, sd.shape)).values)
[ 1.25 1.5 1.75 2. 1.75 1.5 1.25]
[ 0.5 1. 1.5 2. 1.5 1. 0.5]
[ 0.0875 0.775 0.5625 2.55 0.7125 0.325 0.0375]
[ 1.5 3. 4.5 6. 4.5 3. 1.5]
The spectral distribution can be normalised with an arbitrary factor:
print(sd.normalise().values)
print(sd.normalise(100).values)
[ 0.25 0.5 0.75 1. 0.75 0.5 0.25]
[ 25. 50. 75. 100. 75. 50. 25.]
A the heart of the colour.SpectralDistribution class is the
colour.continuous.Signal class which implements the
colour.continuous.Signal.function method.
Evaluating the function for any independent domain \(x \in \mathbb{R}\) variable returns a corresponding range \(y \in \mathbb{R}\) variable.
It adopts an interpolating function encapsulated inside an extrapolating
function. The resulting function independent domain, stored as discrete
values in the colour.continuous.Signal.domain attribute corresponds
with the function dependent and already known range stored in the
colour.continuous.Signal.range attribute.
Describing the colour.continuous.Signal class is beyond the scope of
this tutorial but the core capability can be described.
import numpy as np
range_ = np.linspace(10, 100, 10)
signal = colour.continuous.Signal(range_)
print(repr(signal))
Signal([[ 0., 10.],
[ 1., 20.],
[ 2., 30.],
[ 3., 40.],
[ 4., 50.],
[ 5., 60.],
[ 6., 70.],
[ 7., 80.],
[ 8., 90.],
[ 9., 100.]],
interpolator=KernelInterpolator,
interpolator_kwargs={},
extrapolator=Extrapolator,
extrapolator_kwargs={u'right': nan, u'method': u'Constant', u'left': nan})
# Returning the corresponding range *y* variable for any arbitrary independent domain *x* variable.
signal[np.random.uniform(0, 9, 10)]
array([ 94.74700025, 50.62829102, 72.93120155, 81.86179968,
70.14736394, 83.11336665, 51.17649751, 71.00638621,
86.94761009, 78.01845818])
Convert to Tristimulus Values#
From a given spectral distribution, CIE XYZ tristimulus values can be calculated:
sd = colour.SpectralDistribution(data_sample)
cmfs = colour.MSDS_CMFS["CIE 1931 2 Degree Standard Observer"]
illuminant = colour.SDS_ILLUMINANTS["D65"]
# Calculating the sample spectral distribution *CIE XYZ* tristimulus values.
XYZ = colour.sd_to_XYZ(sd, cmfs, illuminant)
print(XYZ)
[ 10.97085572 9.70278591 6.05562778]
From CIE XYZ Colourspace#
CIE XYZ is the central colourspace for Colour Science from which many computations are available, expanding to even more computations:
# Displaying objects interacting directly with the *CIE XYZ* colourspace.
pprint(colour.COLOURSPACE_MODELS)
('CAM02LCD',
'CAM02SCD',
'CAM02UCS',
'CAM16LCD',
'CAM16SCD',
'CAM16UCS',
'CIE XYZ',
'CIE xyY',
'CIE Lab',
'CIE Luv',
'CIE UCS',
'CIE UVW',
'DIN99',
'Hunter Lab',
'Hunter Rdab',
'ICaCb',
'ICtCp',
'IPT',
'IPT Ragoo 2021',
'IgPgTg',
'Jzazbz',
'OSA UCS',
'Oklab',
'hdr-CIELAB',
'hdr-IPT',
'Yrg')
Convert to Display Colours#
CIE XYZ tristimulus values can be converted into sRGB colourspace RGB values in order to display them on screen:
# The output domain of *colour.sd_to_XYZ* is [0, 100] and the input
# domain of *colour.XYZ_to_sRGB* is [0, 1]. It needs to be accounted for,
# thus the input *CIE XYZ* tristimulus values are scaled.
RGB = colour.XYZ_to_sRGB(XYZ / 100)
print(RGB)
[ 0.45675795 0.30986982 0.24861924]
# Plotting the *sRGB* colourspace colour of the *Sample* spectral distribution.
plot_single_colour_swatch(ColourSwatch(RGB, "Sample"), text_kwargs={"size": "x-large"})

Generate Colour Rendition Charts#
Likewise, colour values from a colour rendition chart sample can be computed.
Note
This is useful for render time checks in the VFX industry, where a synthetic colour chart can be inserted into a render to ensure the colour management is acting as expected.
The colour.characterisation sub-package contains the dataset for
various colour rendition charts:
# Colour rendition charts chromaticity coordinates.
print(sorted(colour.characterisation.CCS_COLOURCHECKERS.keys()))
# Colour rendition charts spectral distributions.
print(sorted(colour.characterisation.SDS_COLOURCHECKERS.keys()))
['BabelColor Average', 'ColorChecker 1976', 'ColorChecker 2005', 'ColorChecker24 - After November 2014', 'ColorChecker24 - Before November 2014', 'TE226 V2', 'babel_average', 'cc2005', 'cca2014', 'ccb2014']
['BabelColor Average', 'ColorChecker N Ohta', 'ISO 17321-1', 'babel_average', 'cc_ohta']
Note
The above cc2005, babel_average and cc_ohta keys are
convenient aliases for respectively ColorChecker 2005, BabelColor Average
and ColorChecker N Ohta keys.
# Plotting the *sRGB* colourspace colour of *neutral 5 (.70 D)* patch.
patch_name = "neutral 5 (.70 D)"
patch_sd = colour.SDS_COLOURCHECKERS["ColorChecker N Ohta"][patch_name]
XYZ = colour.sd_to_XYZ(patch_sd, cmfs, illuminant)
RGB = colour.XYZ_to_sRGB(XYZ / 100)
plot_single_colour_swatch(
ColourSwatch(RGB, patch_name.title()), text_kwargs={"size": "x-large"}
)

Colour defines a convenient plotting object to draw synthetic colour rendition charts figures:
plot_single_colour_checker(
colour_checker="ColorChecker 2005", text_kwargs={"visible": False}
)

Convert to Chromaticity Coordinates#
Given a spectral distribution, chromaticity coordinates CIE xy can be computed
using the colour.XYZ_to_xy definition:
# Computing *CIE xy* chromaticity coordinates for the *neutral 5 (.70 D)* patch.
xy = colour.XYZ_to_xy(XYZ)
print(xy)
[ 0.31259787 0.32870029]
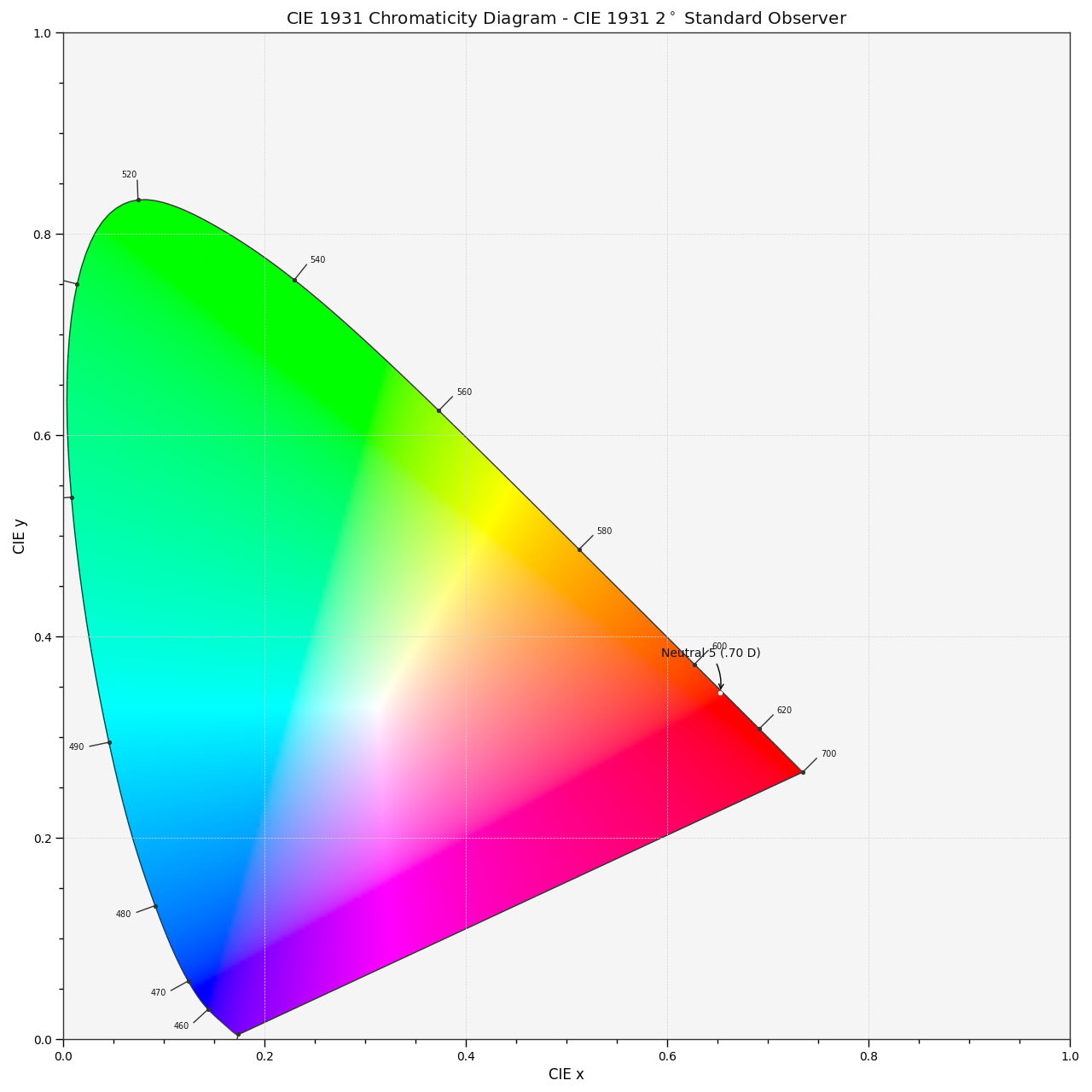
Chromaticity coordinates CIE xy can be plotted into the CIE 1931 Chromaticity Diagram:
import matplotlib.pyplot as plt
# Plotting the *CIE 1931 Chromaticity Diagram*.
# The argument *show=False* is passed so that the plot doesn't get
# displayed and can be used as a basis for other plots.
plot_chromaticity_diagram_CIE1931(show=False)
# Plotting the *CIE xy* chromaticity coordinates.
x, y = xy
plt.plot(x, y, "o-", color="white")
# Annotating the plot.
plt.annotate(
patch_sd.name.title(),
xy=xy,
xytext=(-50, 30),
textcoords="offset points",
arrowprops=dict(arrowstyle="->", connectionstyle="arc3, rad=-0.2"),
)
# Displaying the plot.
render(
show=True,
limits=(-0.1, 0.9, -0.1, 0.9),
x_tighten=True,
y_tighten=True,
)
See More#
The Basic Usage page puts an emphasis on basic but important to understand concepts of Colour.
The Advanced Usage page describes some advanced usage scenarios of Colour.
The Google Colab How-To guide for Colour shows various techniques to solve specific problems and highlights some interesting use cases.